Đề ôn toán cuối kì I
Đề chính thức
Câu 1. Giải các phương trình, bất phương trình và hệ phương trình sau:
a) \((x - 6)(3x + 9) = 0 \quad ; \quad (3x - 2)(2x + 1) = 0\)
b) \(\begin{cases}2x - y = 4 \\ x + 2y = -3\end{cases} \quad ; \quad \begin{cases}2x + 3y = 15 \\ 3x - y = 6\end{cases}\)
c) \(2x - 18 < 0 \quad ; \quad 4x - 3 \le -2x + 1\)
Câu 2. Tính giá trị các biểu thức:
a) \(A = \sqrt{75} - \sqrt{12} - \sqrt{27}\)
b) \(B = \sqrt{64} + \sqrt{(-8)^2}\)
c) \(C = \sqrt{(\sqrt{5} - 3)^2} + 50 \cdot \sqrt{\tfrac{1}{5}}\)
Câu 3. Rút gọn biểu thức sau:
a) \(3\sqrt{3a} + 4\sqrt{12a} - 5\sqrt{27a}\)
b) \(2(\sqrt{x} + \sqrt{y}) - \dfrac{x - y}{\sqrt{x} + \sqrt{y}} \quad (x > 0, y > 0)\)
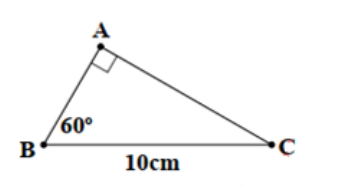
Câu 4. Cho hình vẽ bên, biết \(BC = 10\) cm, góc \(B\) bằng \(60^\circ\).
a) Tính số đo của góc \(C\).
b) Tính độ dài cạnh \(AB, AC\).
c) Vẽ tia phân giác \(BD\). Tính độ dài đoạn thẳng \(DC\).
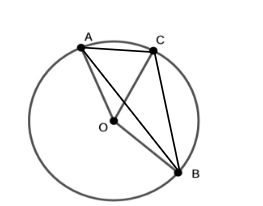
Câu 5. Cho đường tròn tâm \(O\). Biết điểm \(A, B\) và \(C\) cùng thuộc đường tròn. Hãy liệt kê tất cả các góc ở tâm và góc nội tiếp.
Câu 6. Cho đường tròn \((O)\) và dây cung \(BC\). Biết góc \(\widehat{OBC} = 40^\circ\). Lấy điểm \(A\) nằm trên cung nhỏ \(BC\).
a) Tính số đo góc \(\widehat{BAC}\).
b) Vẽ đường kính \(BD\). Biết \(AD = 5\) cm. Tính độ dài cung \(CD\).
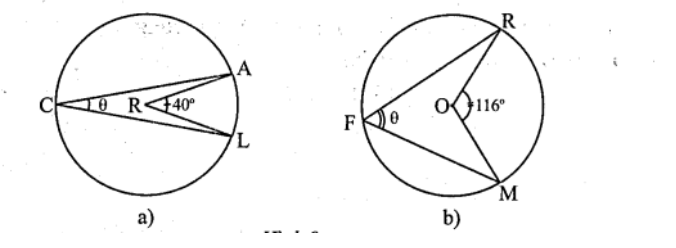
Câu 7. Tìm số đo các cung nhỏ \(\widehat{AL}, \widehat{RM}\) và số đo \(\theta\) của góc nội tiếp tương ứng trong mỗi hình sau:
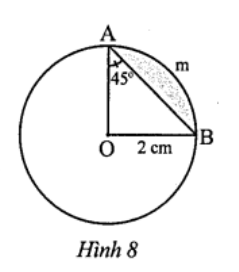
Câu 8. Quan sát Hình 8 và tính:
a) Số đo cung \(AmB\).
b) Độ dài cung \(AmB\).
c) Diện tích hình quạt tròn \(OAmB\).
d) Diện tích hình viên phân giới hạn bởi cung \(AmB\) và dây \(AB\).
Câu 9. Cho điểm \(A\) ngoài đường tròn tâm \((O; 4\ \text{cm})\) thỏa mãn \(OA = 6\) cm. Kẻ hai tiếp tuyến \(AB\) và \(AC\) với đường tròn \((O)\) (B và C là các tiếp điểm). Gọi \(H\) là giao điểm của \(AO\) và \(BC\).
a) Chứng minh: \(AO\) vuông góc với \(BC\) tại \(H\).
b) Tính độ dài dây \(BC\) (kết quả không làm tròn số).
Câu 10. Cho điểm \(A\) nằm ngoài đường tròn \((O; R)\). Vẽ đường tròn đường kính \(AO\) cắt đường tròn \((O; R)\) tại hai điểm \(B\) và \(C\).
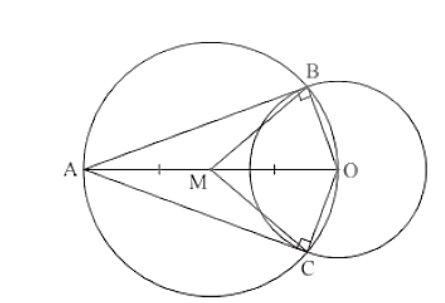
a) Chứng minh \(AB\) và \(AC\) là các tiếp tuyến của đường tròn \((O; R)\).
b) Chứng minh \(AB = AC\).
c) Xác định tia phân giác của \(\widehat{BAC}\) và \(\widehat{BOC}\).
Câu 11. Cho đường tròn \((O; R)\) và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(D\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE\). Chứng minh rằng:
a) \(MA \cdot MB = MC \cdot MD\).
b) Tứ giác \(ABEC\) là hình thang cân.
